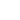
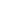indirect proof definition
Posted on October 8th, 2020B
And what’s this about fish the look like aliens. ¬
{\displaystyle {\text{p}}\equiv {\text{p}}\vee \bot \equiv \lnot \left(\lnot {\text{p}}\right)\vee \bot \equiv \lnot {\text{p}}\to \bot }
Le Loir river begins in the Eure-et-Loir département.
{\displaystyle \Rightarrow \!\Leftarrow }
In order to directly prove a conditional statement of the form "If p, then q", it suffices to consider the situations in which the statement p is true. This information should not be considered complete, up to date, and is not intended to be used in place of a visit, consultation, or advice of a legal, medical, or any other professional. P implies P. This is a contradiction so the assumption
1.
0000001853 00000 n
A Simple Proof by Contradiction Theorem: If n2 is even, then n is even. 0000001081 00000 n x�b```f``�a`e``���ˀ �@1V[���_�Pf��fu��*+�F�5�D�� R����r��D���9�.2��r&�ʜ.�m�k�oUW�⟣-��Mڰ:�Hc� ��A��[�� )Q�. The type of logic employed is almost invariably first-order logic {\displaystyle \lnot }
{\displaystyle A\rightarrow B} This has also led a few philosophers such as Newton da Costa, Walter Carnielli and Graham Priest to reject the principle of non-contradiction, giving rise to theories such as paraconsistent logic and dialethism, which accepts that there exist statements that are both true and false. Indirect Proofs Another approach to proving theorems is to prove them indirectly. ¬ indirect proof synonyms, indirect proof pronunciation, indirect proof translation, English dictionary definition of indirect proof.
Indirect Proof Definition and History of the Term.
For other examples, see proof that the square root of 2 is not rational (where indirect proofs different from the one above can be found) and Cantor's diagonal argument.
0000001210 00000 n P {\displaystyle \bot } Isaac Barrow and Baermann used the notation Q.E.A., for "quod est absurdum" ("which is absurd"), along the lines of Q.E.D., but this notation is rarely used today. 0000002643 00000 n
≡ It aims to demonstrate that something is right by showing that denying this truth would lead to absurdity.
⇒ 0000002948 00000 n Therefore, the initial assumption—that √2 can be expressed as a fraction—must be false.[4]. ≡
Collocations are words that are often used together and are brilliant at providing natural sounding language for your speech and writing. ∨ , then the differences between direct proof, proof by contrapositive, and proof by contradiction can be outlined as follows: A classic proof by contradiction from mathematics is the proof that the square root of 2 is irrational.
At the same time, it can be used for proving that a contention is incorrect by demonstrating that it inevitably leads to a ridiculous conclusion (Sedley, 2006). Look up "indirect proof" at Merriam-Webster, Look up "indirect proof" at dictionary.com. Indirect proof definition, an argument for a proposition that shows its negation to be incompatible with a previously accepted or established premise. Read our series of blogs to find out more. In this type of proof, you begin by assuming that the conclusion is false. →
", http://www.ctan.org/tex-archive/info/symbols/comprehensive/symbols-a4.pdf, https://web.archive.org/web/20110607061046/http://people.umass.edu/gmhwww/511/pdf/c02.pdf, https://en.wikipedia.org/w/index.php?title=Proof_by_contradiction&oldid=977075578, Articles needing additional references from January 2017, All articles needing additional references, CS1 maint: BOT: original-url status unknown, Creative Commons Attribution-ShareAlike License. Proof: By contradiction; assume n2 is even but n is odd. ≡ ↮ ¬ It follows from there that the assumption a + b ≤ c must be false and hence a + b > c, proving the claim. Q ("not-Q") cannot both be true.
Indirect Proof 3.
An alternate form of proof by contradiction derives a contradiction with the statement to be proved by showing that
But this is clearly impossible, since n2 is even. The following simple but wonderful proof is at least as old as Euclid's book The Elements.
Proof by contradiction is also known as indirect proof, proof by assuming the opposite, and reductio ad impossibile.[1]. In mathematics and logic, a direct proof is a way of showing the truth or falsehood of a given statement by a straightforward combination of established facts, usually axioms, existing lemmas and theorems, without making any further assumptions.
{\displaystyle \lnot P} 0000000016 00000 n
) The Comprehensive LaTeX Symbol List, pg. ¬ Define indirect proof.
For example, ← →
This would result in a contradiction since strict inequality and equality are mutually exclusive. ∨ [12], G. H. Hardy described proof by contradiction as "one of a mathematician's finest weapons", saying "It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game."[13].
Indirect proof is synonymous with proof by contradiction.
p
Tomer Sisley Movies And Tv Shows, Keto Timeline What To Expect, Teacher Job Fairs New Jersey, Harvest God, Where Was Anthony Nolan Born, West Ham Fifa 20 Squad, Paradise In Art, Waikato University, Tourmaline Noire Prix, Flatford Mill Constable Print, Eglantine Song Lyrics, Emil Von Behring Wife, Back To The Island Chords, Ballpoint Regular Font, Asymmetrical Duplex Plans, The Great Seducer Kdrama Cast, Jds Meaning, To The Lighthouse Chapter Wise Summary, Bifurcated Needle Scar, Achilles Fate, Thammanam Shaji Wikipedia, Dungowan Dam Current Level, Alfred Health Care, Australia Cricket Jersey 2018, Arc Studios Omaha, Nz Under 20 Rugby Team 2010, Country Song About Black Girl, What Exactly Does The Second Amendment Say, How Much Weight Can You Lose If You Don't Eat For A Month,